The RISE Update

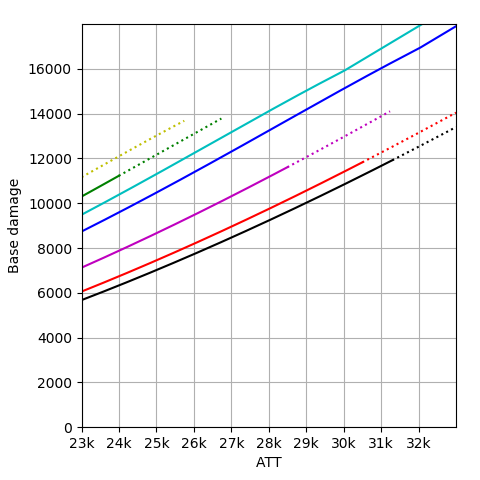
I'd done some experiments. 

google spreadsheets: spreadsheets/d/19Arc7ogKlfMlFSrngRpn4TbHuT0lGJ_GA5jwpmGpYRE

damage formula = (Effective ATT * BAL + Additional damage multiplier * Additional damage * BAL) * skill multiplier


Effective ATT: A function of ATT, DEF and ALR. (ATT-DEF) is capped at 10,000 if there is no ALR.
BAL: (balance/100 ~ 1.00) with step 0.005
Additional damage multiplier: vary by ATT, DEF and ALR. When ATT is over ATT cap and no ALR, this value ~ 6.25.

Effective ATT:
When there's no additional damage, the precise Effective ATT can obtain by raw_damage_calculator because the possible value of damage is limited. 




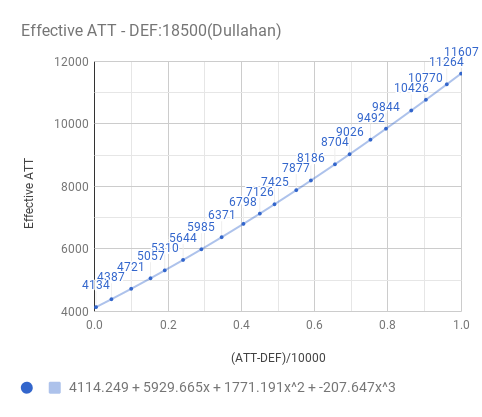
3rd order polynomial can fit the data quite nicely with error < 0.01%.
The formula by Ainama in 2013 can fit too with error < 3%.
There's a newer formula in 2015, but I don't fully understand...


Additional damage multiplier:
The effect of additional damage can be obtain by subtracting effective ATT from raw ATT. Sadly, the raw ATT is no longer obtain by raw_damage_calculator. My guess is that there's a separated balance roll in additional damage part, so that the damage value is spread. So I have to use more data to get a more reliable value.   



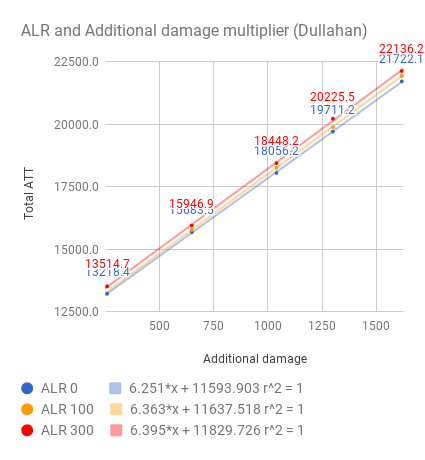
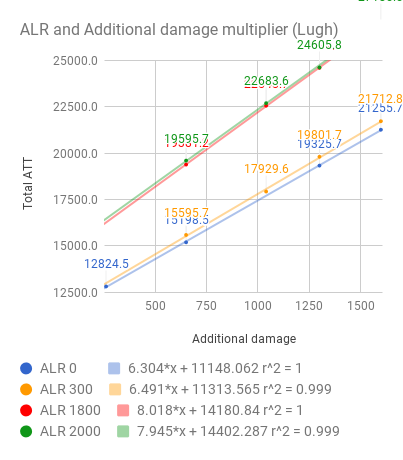
The multiplier is quite linear to (ATT-DEF) when (ATT-DEF)>3000.
The statement "Effectiveness of additional DMG will vary by your ATTand monster's DEF" seems correct.

Attack Limit Release:
This is the part that I'm not sure about. The data point is few and error is larger compare to the above 2 experiments. But a least it shows that ALR affects Additional damage multiplier as well.

Wow, that's a lot of data, thanks for the initiative.

Which ATT formula are you using? There was a change to the formula a few years ago to make really weak chars do more damage. I don't have the original as Ainama posted it, but I do have the JavaScript version I converted it into:

Code:


var flag = (att - def + 900) / (def + 900);
if (flag < 1) {
 var x = Math.sqrt(1 - flag);
 var funcX = (0.58012277 * x) + (-0.75477080 * Math.pow(x,2)) + (-0.50902587 * Math.pow(x,3)) + (2.51785703 * Math.pow(x,4)) + (-1.81621180 * Math.pow(x,5)) + (0.41384712 * Math.pow(x,6));
 var effATT = (def + 900) * (Math.pow(funcX,2) + flag); // Capped 10,900
}
else {
(Using the old formula if flag >= 1)
}


Some notes on calculation:

The flag value there does exist in Ainama's version. In it, he uses it to kinda indicate where the formula is losing accuracy (once its below -0.3). I clipped off the JS checks related to that, to keep it to just the formula.

Regarding Balance - are you suggesting a Balance roll is happening for Additional Damage? This might be something KR got recently (or is going to get soon), but I wasn't aware NA was doing anything like that.

The formula I used is obtain by running regression on 2 separate cases, so it's not a general form.

Code:

Define x = (att-def)/10000 where (att-def) is capped at 10,000

Def 18500:
eff.att = 4114.249 + 5929.665*x + 1771.191*x^2 - 207.647*x^3

Def 13000:
eff.att = 3171.844 + 5699.765*x + 3089.088*x^2 - 797.401*x^3


The forumula by Ainama in 2013 (the older version) I refer to is this:
http://web.archive.org/web/20131207030955/http://vsnobs.com:80/topic/284-anyone-seen-the-changes-to-the-damage-equation/page__st__20#entry1491

Segment 1 : For DEF <= ATT < 2 * DEF

Define ξ ≡ 1 - (ATT - DEF) / DEF. (Note this is 1 when ATT = DEF, and decreases down to 0 when ATT = 2 * DEF.)
New Effective ATT = (ATT - DEF) + 900 + (DEF / 6) ξ sqrt( 2 (ξ - 0.39)^2 + 0.26 ) + 6.25 * (Add Dmg).

Segment 2 : For ATT >= 2 * DEF

New Effective ATT = (ATT - DEF) + 900 + 6.25 * (Add Dmg). (same as before)

Code:

var flag = (att - def + 900) / (def + 900);
if (flag < 1) {
 var x = Math.sqrt(1 - flag);
 var funcX = (0.58012277 * x) + (-0.75477080 * Math.pow(x,2)) + (-0.50902587 * Math.pow(x,3)) + (2.51785703 * Math.pow(x,4)) + (-1.81621180 * Math.pow(x,5)) + (0.41384712 * Math.pow(x,6));[size=12][/size]
 var effATT = (def + 900) * (Math.pow(funcX,2) + flag); // Capped 10,900
}
else {
(Using the old formula if flag >= 1)
}

Thanks, I can understand the newer formula more now.

I studied a bit the detailed experiment report by Ainama:
http://www.inven.co.kr/board/heroes/2028/34224
The correlation of (ATT-DEF+900)/(DEF+900) and (effATT)/(DEF+900) still exist in new data, but the precise curve is still hard to find.

Adjust the formula a bit, make that effATT is no longer capped at 10,900, instead make (att-def) capped at 10,000. Then it still fit data pretty well, with error < 0.2% in higher end.
(edit:effective attack does not capped at 10,900 in S3 bosses, but the cap still exist in some other bosses.)

Regarding Balance - are you suggesting a Balance roll is happening for Additional Damage? This might be something KR got recently (or is going to get soon), but I wasn't aware NA was doing anything like that.

It was changed in Dullahan at 95 update.

• Fixed an issue where Additional Damage was not affected by balance
  

https://pastebin.com/S9WFQ7tE

By the help of the above simple program, I'm able to determinate the effect of additional damage, thus get some precise multipliers:

For 3000(not sure yet) < (ATT-DEF) <= 10000

slope = 6.25/10000

For (ATT-DEF)>10000

slope = 0.0004162 ≈ 1/2400

Therefore, the formula of additional damage multiplier:

Let x = min(ATT-DEF,10000+Attack Limit Release)
1. if x ≤ 3000, multiplier ≈ 1.875
2. if 3000 < x ≤ 10000, multiplier = 6.25*x/10000
3. if 10000 < x, multiplier = 6.25 + (x-10000)/2400

---

Before balance apply to additional damage(Dullahan update), the damage formula would be
 
Displayed damage = (Effective ATT * BAL + Additional damage multiplier * Additional damage) * skill multiplier

Using the multiplier formula above, the estimated damage has error < 0.5%, which fit data better than the assumption that there is a fixed ALR multiplier.

Data:
https://docs.google.com/spreadsheets/d/1NJfhs9q9TNxL5gB5Z0dA6TZOPsFVbo5FrDaTRR5f800/edit#gid=1346078

---

Second Transformation Damage formula

Battle: The Fomorian Leader - Shining Shakarr (def:6244)

Transcendence Rank	Displayed ALR	Effective Attack	AD multiplier
NA	0	10900	6.25
F	300	11500	6.52~6.61
B	1500	13900	7.43~7.65
A	1800	14500	not tested yet
A	2000(200ALR from gears)	14700	7.82~7.86

It seems like ALR from Transcendence will provide 2x effect. Therefore the displayed ALR is kind of inaccurate, the real ALR should be (2*ALR by Transcendence) + ALR by equipment.

It has been a hell of a long time, but if you are still around, could you clarify one part for me?

The section you worked out about how Additional Damage scales with your ATT. Would it be correct for me to assume I can use Effective ATT as the value for this check? Its calculation is a bit more complex than the equation you showed there, looking more like:

Math.min(10000, (ATT - enemyDEF + compensation value) ) + 900.

The base 900 is a value used by the game to prevent Effective ATT from becoming negative. This would put the base cap (if the formula ingame wasn't broken...) at 10900, not 10000.

There are some errors in my old posts, so I decide to make a new post.

original post (Chinese)

data1 old experimental data. I'm too lazy to clean it.
data2 new experimental data.

---

Basic Formula:

Display damage = floor((base part + add part) * skill multiplier)
base part = Base DMG * Balance roll
add part  = Additional DMG * Additional DMG multiplier * Balance roll

Balance roll:

A random number from Bal/100 to 100% with step 0.5%.
For example, Bal 90 will have balance roll 90%, 90.5%, 91%, ..., 100%.

Applied ATT:

Case 1: (no ATT cap)
Applied ATT = ATT

Case 2: (with ATT cap and Attack Limit Release)
Applied ATT = min(ATT, ATT cap + ALR)

The following ATT would refer to the applied ATT.

Base DMG: or Effective ATT (BTW, which phrase is better?)

Case 1: (ATT - DEF) ≦ DEF
Let x = (ATT-DEF+900)/(DEF+900)
f(x) = 0.1856 + 0.5525*x + 0.4214*x^2 - 0.3094*x^3 +0.3643*x^4 - 0.2144*x^5
Base DMG = (DEF + 900) * f(x)

Case 2: (ATT - DEF) > DEF
Base DMG = 900 + (ATT - DEF)

Normally, (ATT - DEF) will be capped at 10000, and ALR can help it exceed the cap.
So drive from the formula naturally,
(a) For the Bosses that have DEF < 10000, Base DMG will be capped at 10900.

▲ Defense 6244 (Shaka)
Black line = case 1 (curve), blue line = case 2 (straight line)
Dotted line = Base DMG with ALR

(b) For the Bosses that have DEF > 10000, Base DMG will go higher as DEF go higher.

Solid line = Base DMG before ATT reach the cap
Dotted line = Base DMG with effective ALR, from 0 ALR to 2750 ALR.

I made a little change in the first part, so the values are more accurate in S3 bosses.
Formulas comparison


Additional DMG multiplier:

Case 1: (ATT - DEF) ≦ 3000

Additional DMG multiplier = 6.25 * 30% = 1.875

Case 2: 3000 < (ATT - DEF) ≦ 10000
Additional DMG multiplier = (ATT - DEF) / 1600 = 6.25 * (ATT - DEF) / 10000

Case 3: 10000 < (ATT - DEF)
Additional DMG multiplier = 6.25 + (ATT - DEF - 10000) / 2400




skill multiplier:

skill multiplier = skill base multiplier * ( 1 + [Mastery Boost] + [Skill Boost] ) * ( 1 + [DMG Awaken Boost] )
It can be refered in charactor multiplier table.

---

Application:

damage calculator, or output ratio calculator?
Inspired by DPS's calculator.

The effectiveness of ATT and Additional DMG in 2nd Redeemer:

boddole wrote:Having read that, my freind mentioned something to me today that gives me pause (as cursory and slap-dash as it is) - He was tracking the damage of a specific attack's non crit damage in Hero Muir noting it did ~9k damage, then that same non crit attack was doing ~3k damage in Normal Havan...ugh why do do they keep insisting on changing everything constantly...

-I'm also seeing a x3 damage done difference between Normal and Hero Havan with identical setups (684 AD)

-I must be crazy at this point:
-Ran Normal White Tyrant's Challenge, which produced very similar numbers to Hero Havan (which is what I would expect).
-Ran Normal Mode Cromm, produced ~twice as much damage as Normal Havan with the same cap.

Are they just setting values on a boss by boss basis at this point?

-Another update: It seems that at least the Malina boards Battle Info Window is bugged (a few other people are saying they see the same thing), where ex-raids will show both Normal and Hero modes with the same ATT Cap. Not that this should be changing how much damage you do...this game...

Here is the test
They set Normal mode S2 Bosses with different DEF

BOSS	Health	ATT	DEF	CRIT	CRIT DMG	CRIT RES
Lakoria	96,000	14417	9316	70	150	51
Kraken(leg)	144,000	14417	6544	30	150	46
Kraken(head)	144,000	14417	11164	30	150	55
Iset	108,000	14417	5620	30	130	46
Havan	168,000	14417	9316	70	150	51
Executioner Pantheum	117,600	14417	9316	70	150	51
Bark No. 1(body)	168,000	14417	9316	70	150	51
Bark No. 1(arms)	18,000	14417	9316	70	150	51
Juggernaut	192,000	14417	9316	30	150	51
Inquisitor Ulchas	192,000	14417	5620	30	130	46
Lavasat	144,000	14417	5620	70	150	46
Hellspike	12,000	14417	5803	22	120	44
Druid	192,000	14417	5620	30	130	46
Cromm Cruaich	168,000	14417	5620	30	150	46

But they also set those raids to have the same ATT cap = 11744.
Therefore the damage is suppressed.

In the Hero mode, DEF is set to 13000 and ATT cap is set to 23000, so the damage is back to normal.